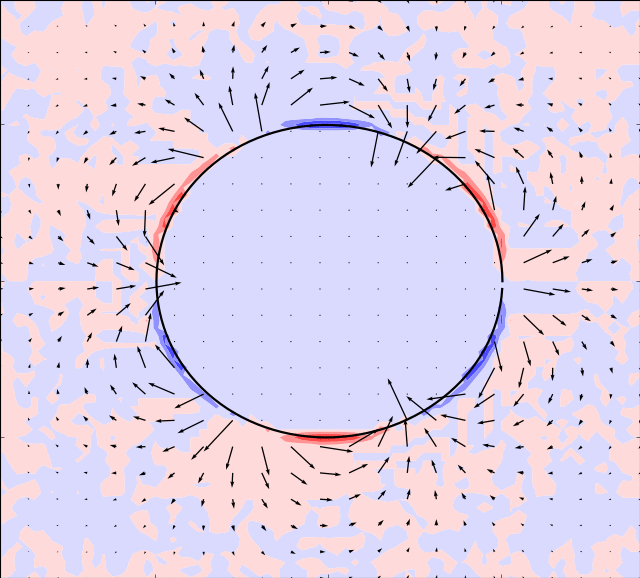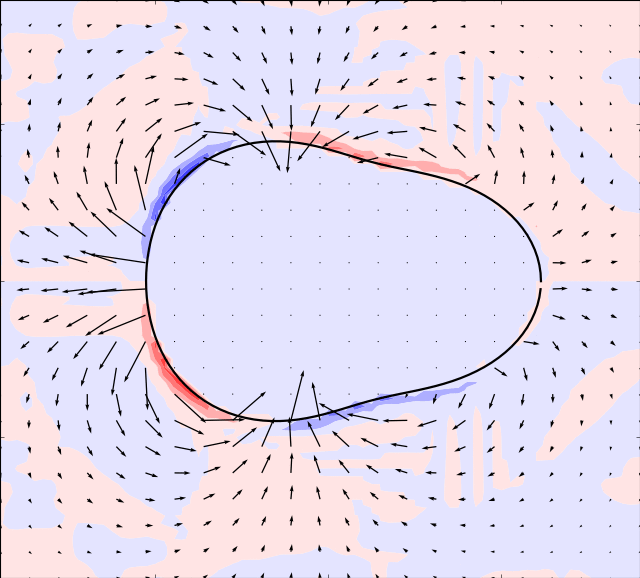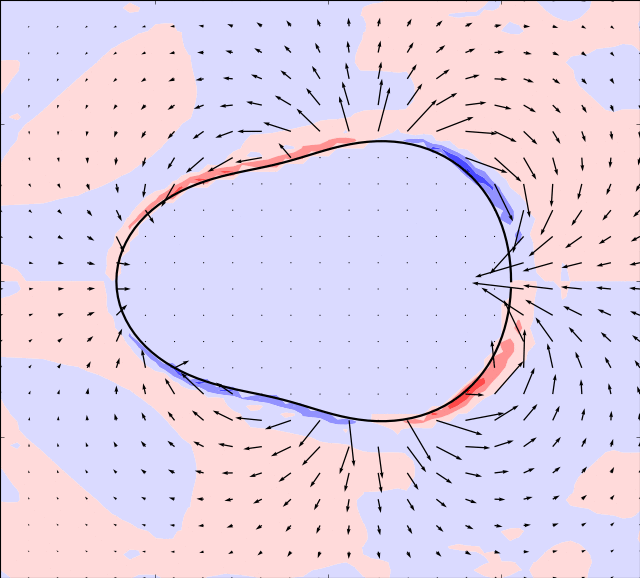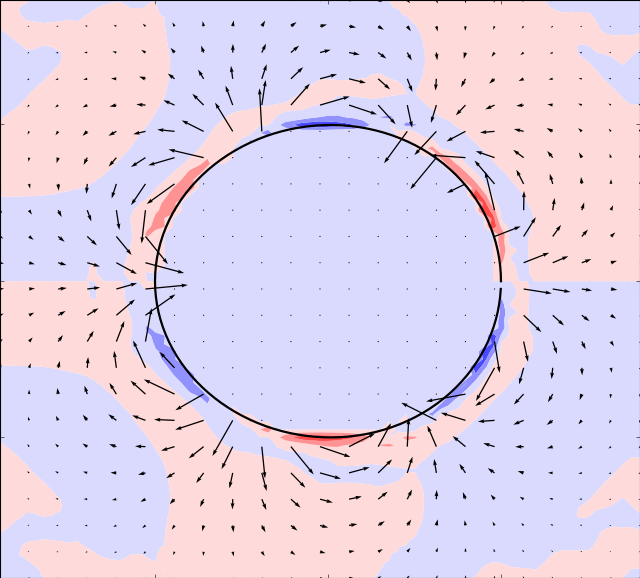
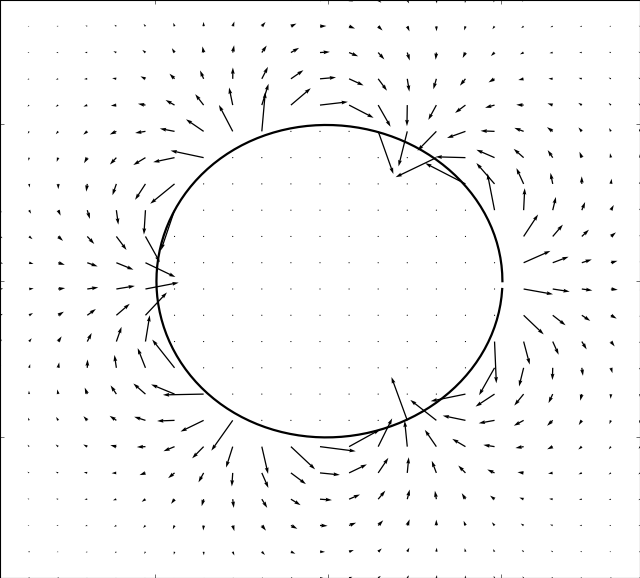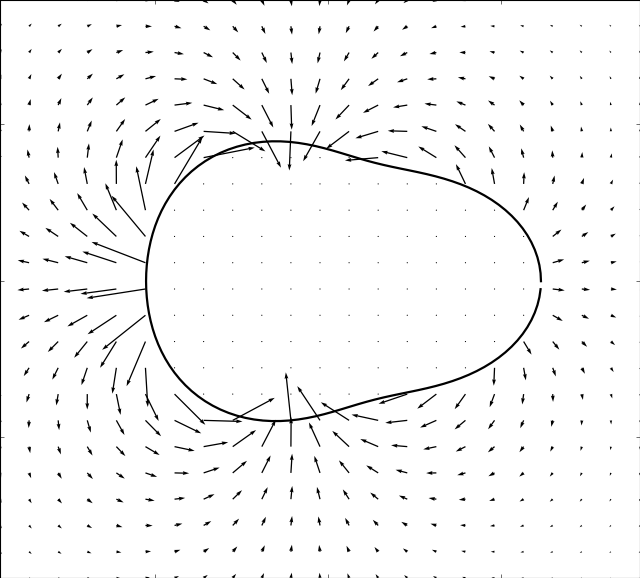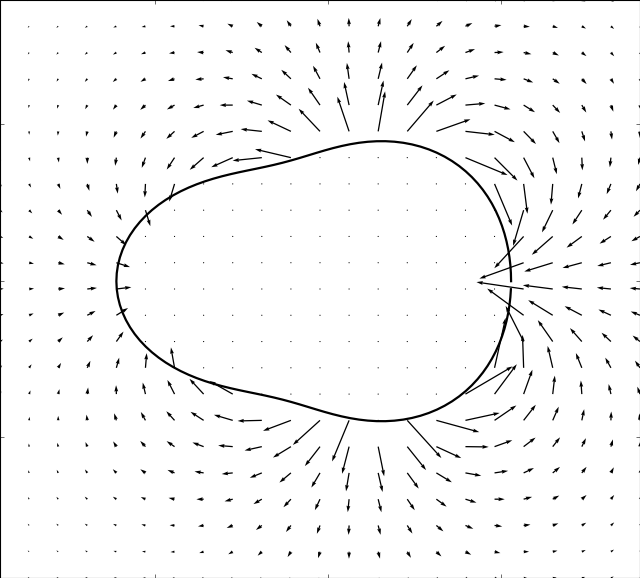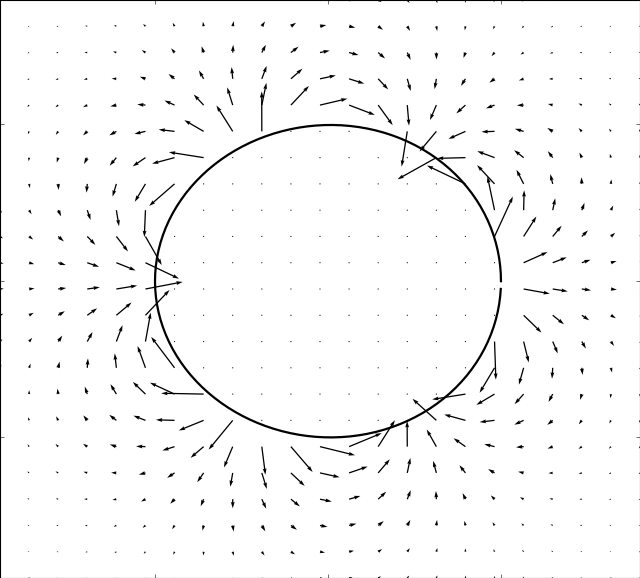
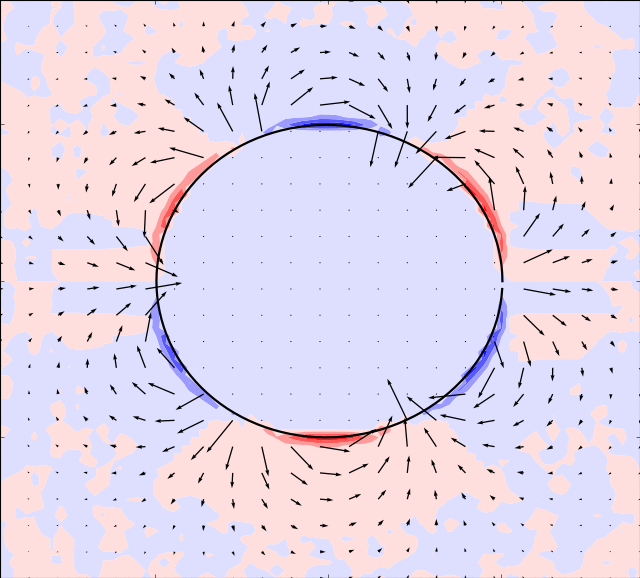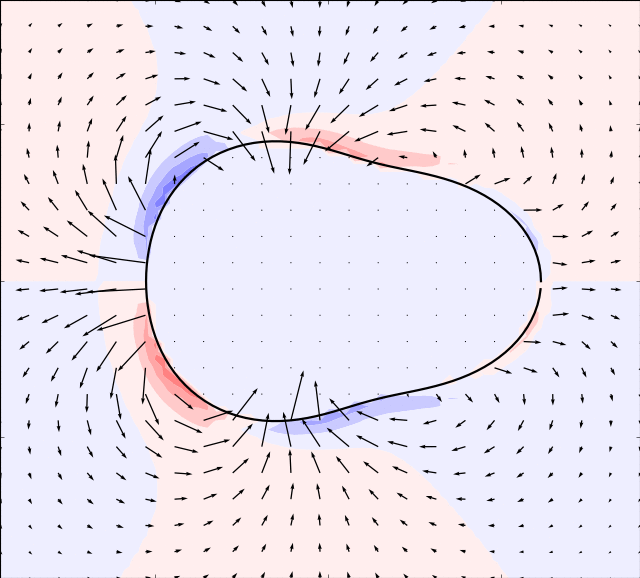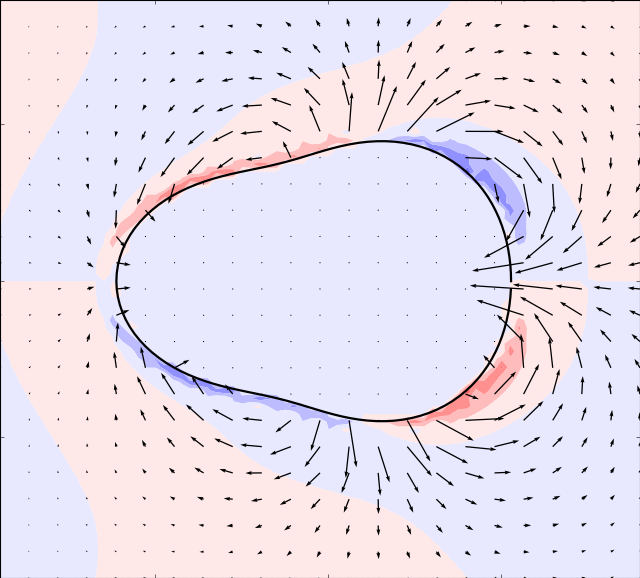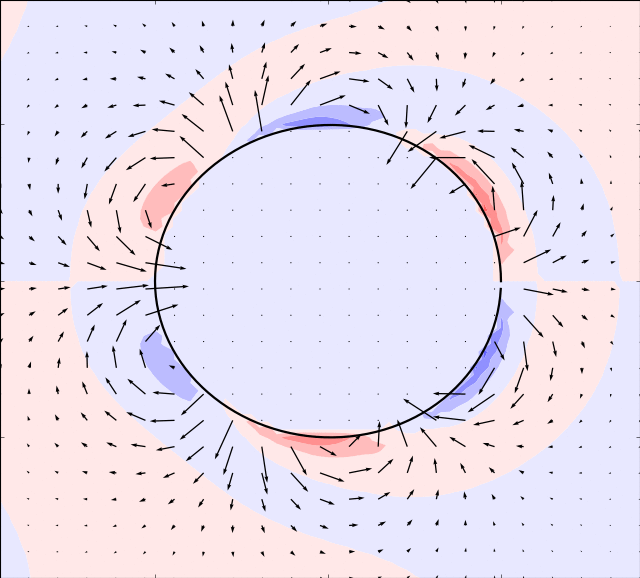
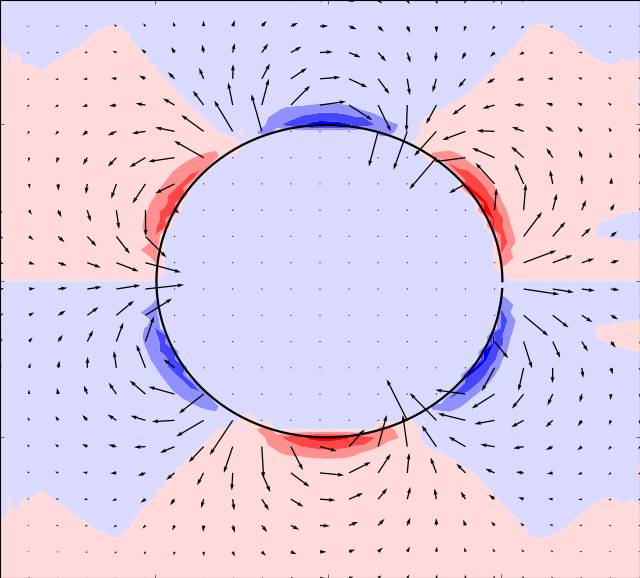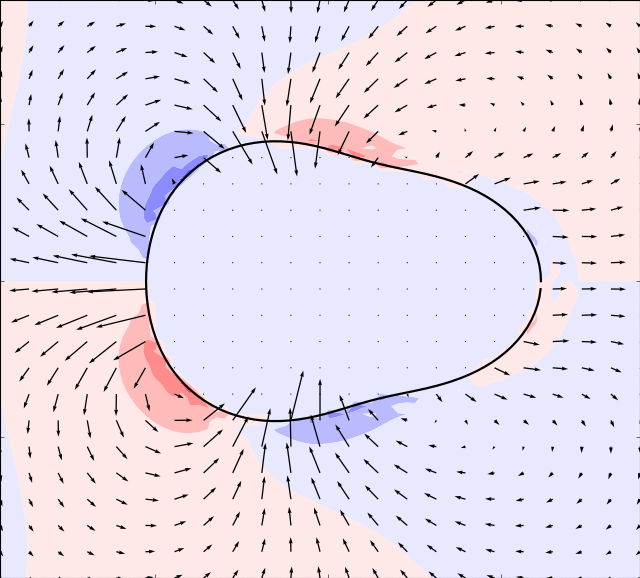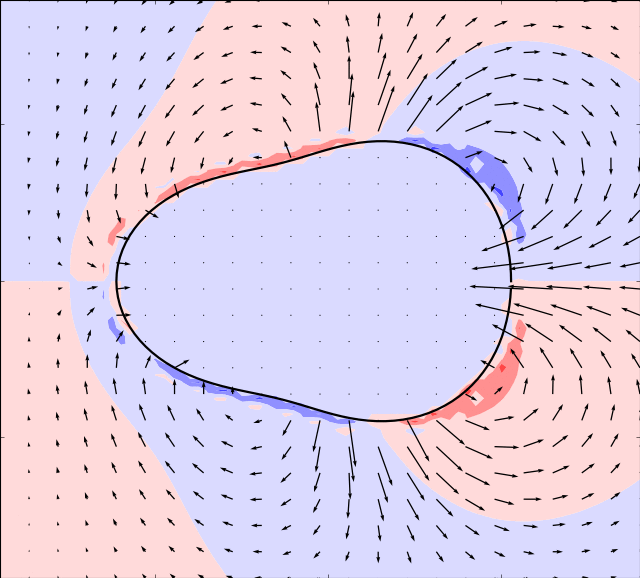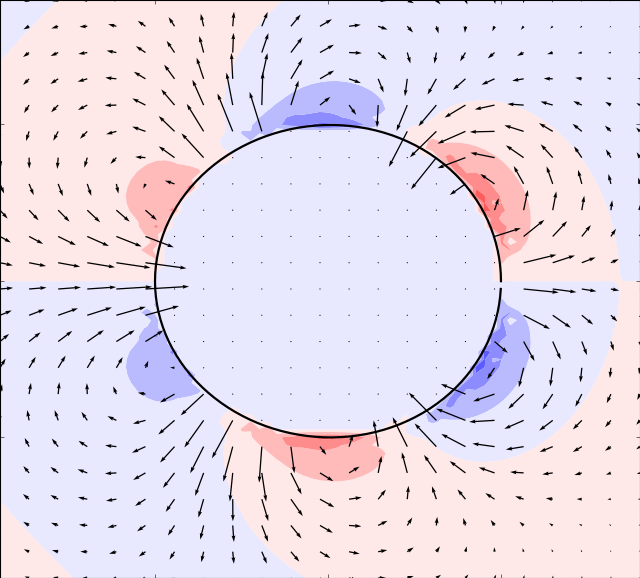
Mason & Burdick Amoeba
Here we take the example given by [MB99]. The boundary is simulated by:
By using an appropriate time evolution of the two shape modes we can achieve forward motion.
In the simulations below, the parameter is set to and the following evolution in time of the shape modes is used
In order for the immersed boundary method to converge we must also ensure that the area enclosed by the boundary remains constant. This can be achieved by adding a normalization:
where
Code
shapevariables = (
lambda t: 1-cos(t),
lambda t: sin(t),
)
epsilon = 0.1
R = lambda s,q: 1 + epsilon*(q[0]*cos(2*s) + q[1]*cos(3*s))
N = lambda s,q: sqrt(1+0.5*epsilon**2*(q[0]**2+q[1]**2))
X = lambda s,q: R(s,q)*cos(s)/N(s,q)
Y = lambda s,q: R(s,q)*sin(s)/N(s,q)
bodies = (
(X,Y),
)