Matrix Multiplication Benchmarks
Insired by this StackOverflow question I decided to run my own benchmarks to compare frameworks like Numpy, Blas and Eigen3 in computational speed. The benchmark that I selected is multiplication of two square matrices. Matrix-matrix multiplication is implemented as sgemm in cblas, and as np.dot in numpy. The versions of the packages used for the benchmarks are listed in the following table.
gcc |
9.1.0-2 |
python |
3.7.3-2 |
python-numpy |
1.16.4-1 |
cblas |
3.8.0-2 |
eigen |
3.3.7-2 |
cuda |
10.1.168-4 |
Given the files cbench.cpp, main.py, and setup.py in the current directory, one can first compile them and then run the benchmarks with the sequence of commands
$ python setup.py build_ext -i
$ python main.py
Results
Two benchmarks are performed - the first is multiplication of two random matrices and the second is multiplication of identity matrices.
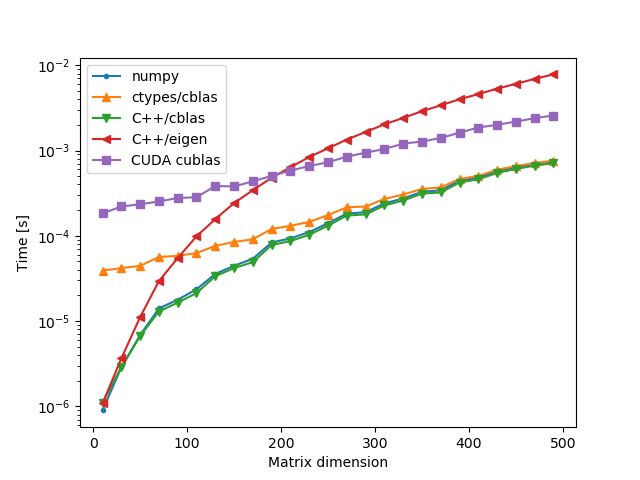
Random Matrices
A = lambda i: np.random.rand(i, i).astype(np.float32)
B = lambda i: np.random.rand(i, i).astype(np.float32)
Identity Matrices
A = lambda i: np.eye(i, dtype=np.float32)
B = lambda i: np.eye(i, dtype=np.float32)
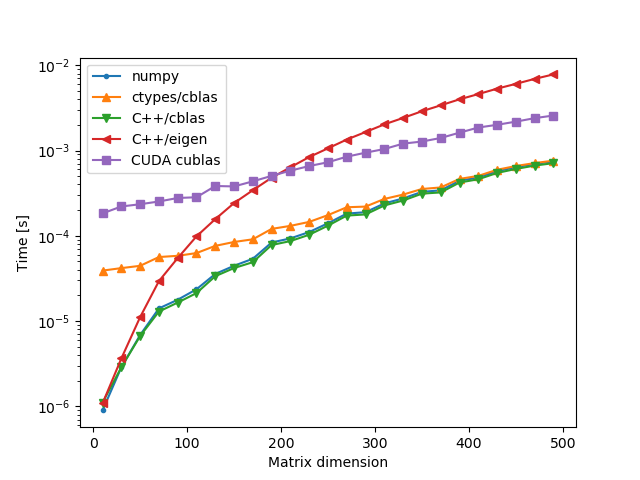
The winners are clearly numpy and C++/cblas. The results for numpy and native calls to cblas are almost identical, which is due to the fact that numpy most likely uses cblas as its backend. Calling cblas via ctypes has a small overhead which is more pronounced for small matrix sizes, but as the matrix size increases the runtime tends to that of the previous two implementations.
The eigen library implementation of matrix multiplication appears to be much slower than the other ones. We have passed the -DNDEBUG and -O3 flags to the compiler but perhaps additional flags are necessary to make eigen competitive with cblas, and even then it would be difficult to compete with the native implementation of cblas which is finely tuned to the local CPU architecture.
The cuda implementation cublas is slowed down by the transfer of data to and from the GPU, as well as the allocation and deallocation of memory on the GPU.